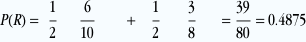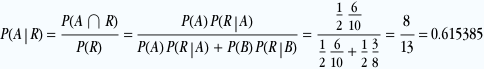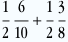|
On considère deux urnes A et B. L’une contient 6 boules rouges et 4 boules noires, l’autre 3 boules rouges et 5 boules noires.

On choisit une urne au hasard et dans cette urne, une boule au hasard.
a) Quelle est la probabilité qu’elle soit rouge ?
b) Sachant que la boule tirée est rouge, quelle est la probabilité qu’elle ait été tirée dans l’urne A ?
a) Soit R=”la boule tirée est rouge”, N=”obtenir une boule noire”, A=”l’urne choisie est la A” et B=”l’urne choisi est la B”.
On recherche P(R)
Il y a deux possibilités pour obtenir une boule rouge: soit elle a été tirée dans l’urne A soit elle a été tirée dans l’urne B. Donc soit on a choisi l’urne A et puis tiré une boule rouge dans l’urne A soit on a choisi l’urne B et ensuite tiré une boule dans l’urne B.
Ce qui peut se traduire en formule:
P(R)=P(A ∩ R)+P(B ∩ R)
P(R)=P(A) P(R|A) + P(B) P(R|B)
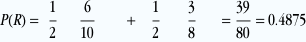
question: en tout, il y a autant de boules rouges (9) que de boules noires. Pourquoi la probabilité d’obtenir une boule rouge est-elle inférieure à 50%?
b) On cherche P(A|R)
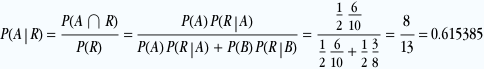
il y a donc plus de chances qu’elle vienne de l’urne A, ce qui est logique puisque la proportion de boules rouges dans l’urne A (60%) et meilleure que dans l’urne B (37,5%)
On peut aussi représenter cela à l’aide d’un arbre
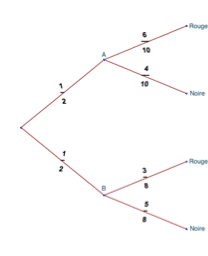
On voit qu’il y a deux chemins pour arriver à “Rouge” correspondant bien au calcul 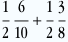
Sous forme de tableau
De manière plus générale, voici ce que donne un arbre de probabilités conditionnelles.
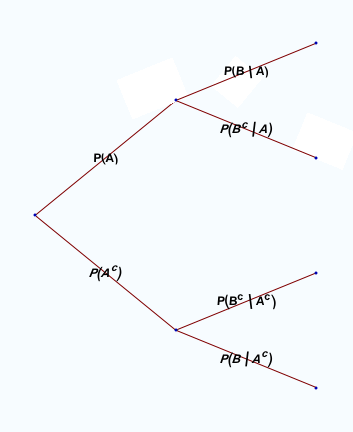
|