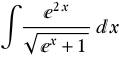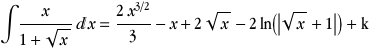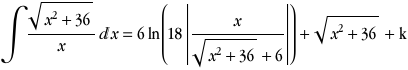|
Intégration par subsitution
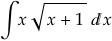
remarque: cette intégrale peut également être faite par parties
On pose t=x+1
On a alors x=t-1
et dx=dt
L'intégrale devient alors
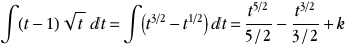
On remplace t par x+1 et on obtient les primitives
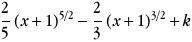
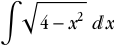
On pose x=2sin t et donc 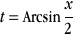
On a alors dx=2cos t dt
et 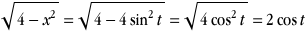
L'intégrale devient alors
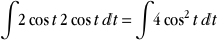
Sachant que 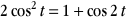 (Carnot), on obtient l'intégrale (Carnot), on obtient l'intégrale
∫2(1+cos 2t)dt=2t+∫2 cos 2tdt=2t+sin 2t+k=2t+2sin t cos t+k
Sachant que 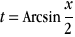 , x=2sin t et , x=2sin t et 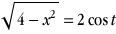 on obtient les primitives on obtient les primitives
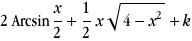
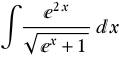
On pose 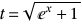 et donc et donc 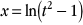
On a alors 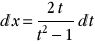
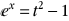
L'intégrale devient alors
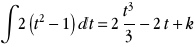
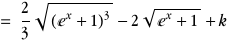
Exercices
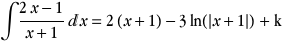
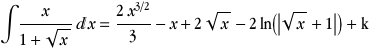
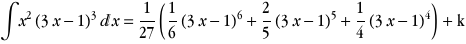
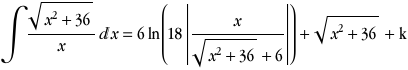
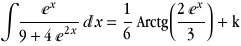
|